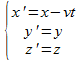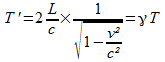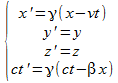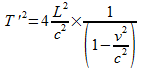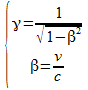Accueil > Cours de Physique > 6ième année > Séminaire de physique en français > 6C La relativité (restreinte)
6C La relativité (restreinte)
mardi 6 novembre 2012 par
Séminaire de physique 2012
Introduction à la relativité
I] Galilée et Newton :
 "Le mouvement est relatif au référentiel d’observation, mais le temps est absolu."
"Le mouvement est relatif au référentiel d’observation, mais le temps est absolu."
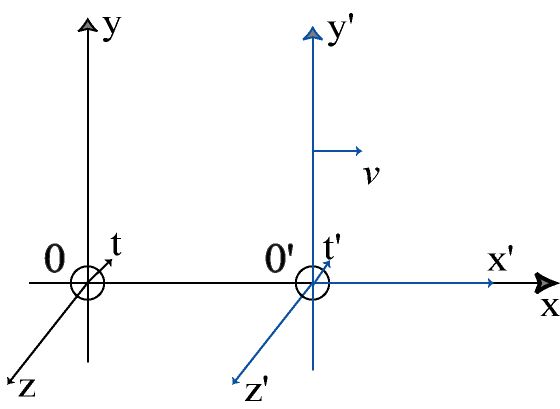
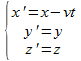 Si on passe d’un référentiel galiléen R à un autre R’ se déplaçant à une vitesse v suivant l’axe des x, alors les nouvelles coordonnées se calculent ainsi :
Si on passe d’un référentiel galiléen R à un autre R’ se déplaçant à une vitesse v suivant l’axe des x, alors les nouvelles coordonnées se calculent ainsi :
Pour Galilée et Newton, le temps s’écoulent à la même vitesse dans les deux référentiels donc t’ = t. La trajectoire du centre d’inertie d’un système ne sera pas la même mais les forces qui s’exercent sur lui, donc son accélération sera la même.
II]Problèmes et paradoxes :
Avec un temps absolu, les forces fondamentales qui s’exercent entre deux objets varient instantanément : si deux corps s’éloignaient l’information "distance" se propagerait à une vitesse infinie pour ajuster la norme de la force.
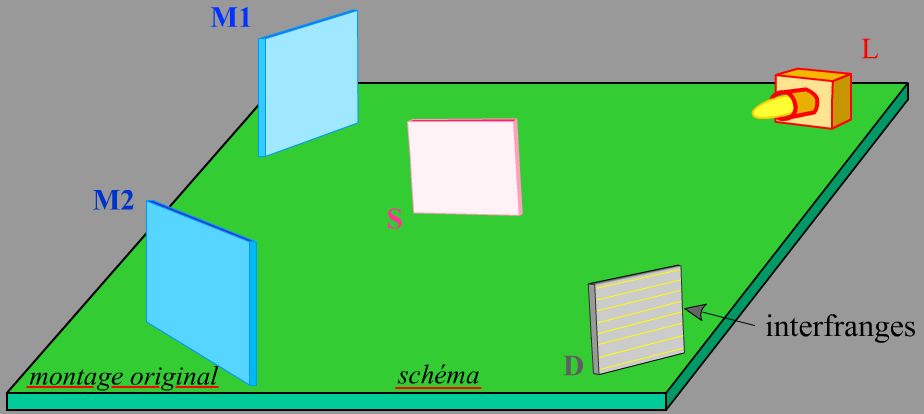
La lumière est une onde, comme le prouvent les expériences de diffractions et d’interférences. Mais dans quel milieu se propage-t-elle entre le Soleil et la Terre ? Henri Poincaré et Christian Huygens proposent un éther pour une onde lumineuse qui serait mécanique, mais ça n’est pas du goût de Maxwell qui a relié l’électricité et le magnétisme.
Albert Michelson et Edward Morley prouvent avec leur interféromètre que l’éther n’existe pas.
III]Notions relativistes
1)Événements simultanés

L’animation flash du train montre bien qu’un signal lumineux envoyé par le contrôleur du milieu arrive en même temps vers les deux contrôleurs à drapeau dans le référentiel lié au train, mais que dans le référentiel lié au sol le rayon lumineux qui va dans la même direction que le train doit mettre plus longtemps à arriver au contrôleur qui s’en éloigne qu’à celui qui s’en approche : Des événements simultanés dans un référentiel ne le sont pas toujours dans un autre.
2)Temps relatif et temps propre
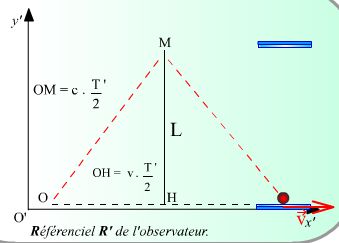
Dans l’animation Flash sur la dilatation du temps, on voit que le temps mis par un photon pour faire un aller-retour est lorsque l’horloge est au repos dans le référentiel lié au sol.
lorsque l’horloge est au repos dans le référentiel lié au sol.Lorsqu’elle est en mouvement la distance à parcourir par un photon est la même (L) dans le référentiel lié à l’horloge mais est plus longue dans le référentiel lié au sol OM² = L² + OH².
La distance OH est la distance parcourue par le miroir dans le référentiel lié au sol OH = vT’/2 pendant une demi-période dans le temps de ce référentiel. Le photon parcourt OM en T’/2 donc OM = cT’/2.
On relie ces équations grâce à Pythagore : OM² = L² + OH² ce qui donne (cT’/2)² = L² + (vT’/2)²
c²T’²/4 = L² + v²T’²/4 T’²(c²-v²) = T’c²(1-v²/c²) = 4L² ce qui donne
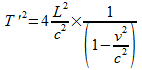 soit
soit 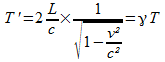 comme v < c on a > 1 donc T’ > T le temps a ralenti pour l’observateur lié au référentiel fixe.
comme v < c on a > 1 donc T’ > T le temps a ralenti pour l’observateur lié au référentiel fixe.
Le temps propre est celui que perçoit le photon ou la particule en mouvement dans son propre référentiel. Pour des particules qui se désintègrent, c’est ce temps propre qui compte pour leur durée de vie.
Question : A quelle vitesse l’horloge doit-elle se déplacer par rapport au sol pour que le temps qu’elle affiche s’écoule deux fois plus lentement que lorsqu’elle est au repos ?
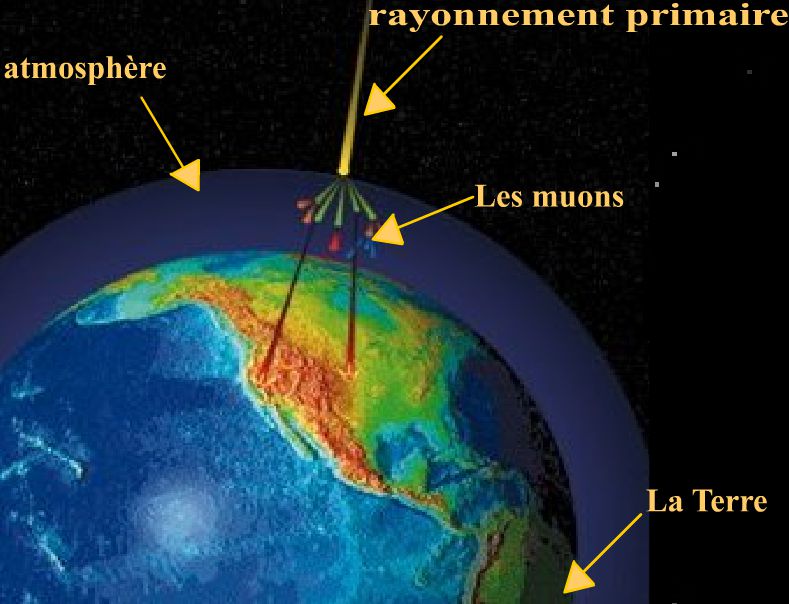
3)Application : la désintégration des muons
Cette animation est un bon exemple pour comprendre que le temps propre des muons est très différent du temps dans le référentiel lié au sol car leur vitesse est proche de celle de la lumière.
En conséquence, ils n’ont pas le temps de se désintégrer lorsqu’ils sont en mouvement (à des vitesses proches de celle de la lumière).
4)Cinématique Relativiste
a)Postulats de la relativité restreinte
Comme en mécanique classique, la masse, la charge et lois physiques ne changent pas si on observe une expérience depuis un autre référentiel. Par contre, on postule que la vitesse de la lumière c ne change pas quand on change de référentiel.
b) Invariant cinématique :
Invariant cinématique :
On choisit l’origine des temps pour les deux référentiels t = t’ = 0s, lorsque O et O’ sont confondus. Un signal lumineux est émis vers un point M. L’instant de réception en M n’est pas la même si le temps ne s’écoule pas à la même vitesse dans les deux référentiels :
![]()
Mais c²t² – x²-y²-z² = c²t’² – x’²-y’²-z’² (= 0 ici) constitue un invariant (est le même dans tous les référentiels.
ds² = c²dt² – dx² – dy² – dz² = cte
c)Transformation de Lorentz (&Fitgerald&Poincaré)
Dans l’espace-temps à 4 dimensions (x, y, z, c.t), la vitesse de la lumière c est constante mais le temps ne s’écoule pas à la même vitesse. Pour changer de référentiel, on utilise la transformation suivante :
|
Pour une vitesse v très inférieure à celle de la lumière c, <<1 donc ²<<<1 ce qui donne |
Exercice : Retrouver la transformation inverse donnant (x, y, z, ct) en fonction de (x’, y’, z’, ct’).
d)Contraction des longueurs :
Pour mesurer dans le référentiel R, la longueur d’une règle en mouvement suivant l’axe des x, on considère deux événements simultanés (x1, t) et (x2, t) pour les deux extrémités de la règle. L = x2-x1.
Dans le référentiel R’ (en mouvement suivant le même axe des x par rapport à R), la règle a une longueur propre L0 différente.
Exercice : Utiliser la transformation de Lorentz pour démontrer la formule ![]() .
.
IV]Relativité générale
Pour A. Einstein, la force de gravité posait problème : comment l’information est-elle transmise pour que la Terre sache à quelle distance elle se trouve du soleil ? Si le Soleil disparaissait, la lumière cesserait de nous parvenir au bout de 8 min environ. La Terre continuerait-elle de tourner autour de rien pendant 8 minutes ?
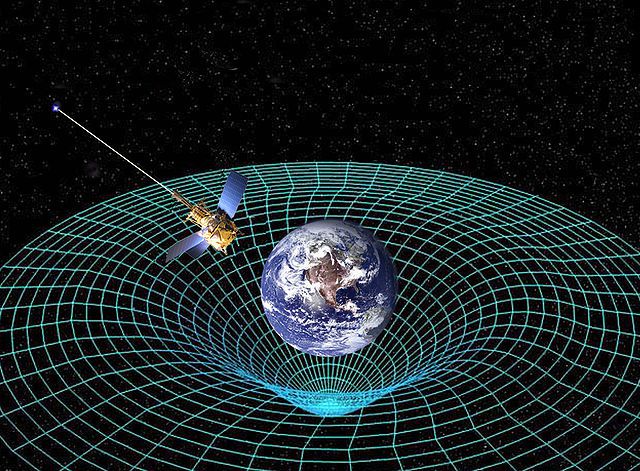
Le problème est résolu en postulant que la masse déforme l’espace-temps comme sur la représentation simplifiée ci-contre : La masse de la Terre crée un puits gravitationnel et le satellite ne fait que suivre une ligne courbe. De plus, plus on se rapproche d’une masse, plus le temps ralenti.

Si c’est l’espace-temps qui est déformé, alors la lumière est aussi déviée par la présence d’un corps massif et peut être piégée lorsque cette masse est trop grande (trou noir). Lors de l’éclipse du 29 mai 1919, Eddington sur une photographie a trouvé une déviation proche des 1,745 secondes d’arc (4,484.10-4 degré).
La précision de la mesure sur une plaque photographique est discutable, mais à l’époque on voulait tellement que cela marche...
Il n’empêche qu’aujourd’hui le GPS doit tenir compte du ralentissement du temps dû au mouvement rapide des satellites et de son accélération due à leur éloignement de la Terre.
Sources : Librement inspiré de http://culturesciencesphysique.ens-lyon.fr/dossiersthematiques/la-relativite
Vous trouverez les animations flash dans les trois articles sur la relativité restreinte.
Documents joints
- dilatation du temps (Flash – 50.4 ko)
- michelson morley (Flash – 221.1 ko)
- muon (Flash – 121.5 ko)
- train (Flash – 138.7 ko)
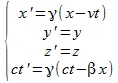 avec
avec  .
.