Pourquoi toujours des sinusoïdes ?

• Parce que c’est la forme d’une onde qui ne comporte qu’une seule fréquence. Toutes les autres formes d’ondes peuvent se construire avec de sinusoïdes.
• Dans la synthèse de Fourier, une forme d’onde se construit avec une sinusoïde à une fréquence fondamentale f₀ et des harmoniques f₁, f₂, f₃, f₄,etc...qui sont des sinusoïdes dont les fréquences sont des multiples de la fréquence fondamentale.

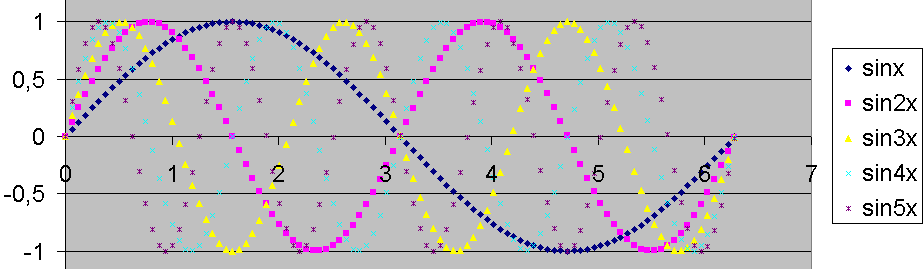
Je veux des preuves !

• Les calculs et démonstrations sont un peu compliquées (voir ici) donc nous nous contenterons de simuler la synthèse d’une forme rectangle.
• La formule théorique est la suivante :
  
  
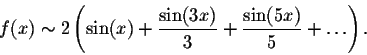
• Dans le tableur on ajoute les harmoniques les uns après les autres et on observe des variations de plus en plus rapides et de plus en plus petite alors que le sinus se transforme progressivement en rectangle :

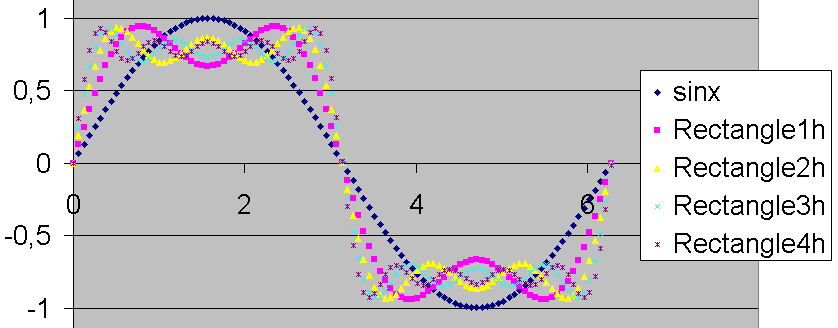
• L’importance des harmoniques diminue rapidement donc on peut se limiter à ceux qui ne sont pas négligeables.
• Pour plus de synthèses, allez voir cette animation flash : on peut choisir des formes classiques ou synthétiser n’importe quelle forme d’onde en modifiant directement les coefficients des harmoniques.
  
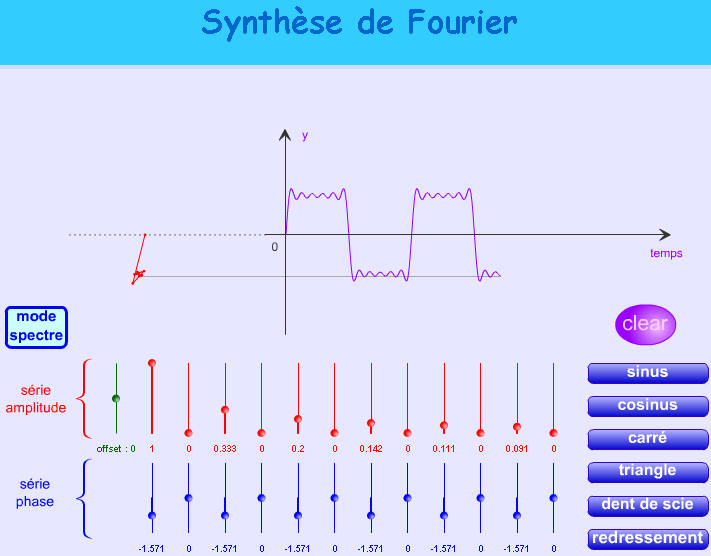
• Le vecteur de Fresnel animé qui dessine la courbe est aussi trèèèès intéressant (à suivre).

Et la musique dans tout cela ?

• Les notes de musiques ont une fréquence fondamentale, une richesse harmonique et une enveloppe temporelle (Voir Notions fondamentales d’acoustique).

1. La note La du diapason (A en notation anglo-saxonne) a une fréquence de 440Hz. Pour changer d’octave il faut multiplier ou diviser par 2 la fréquence.
   
2. Une octave comporte 7 touches blanches et 5 touches noires sur un clavier de piano donc 12 demi-tons. Pour passer à la note suivante (La# ou Ais) il faut multiplier la fréquence par ¹²√2. Ainsi, lorsqu’on passe progressivement du La3 (440Hz) au La4 (880Hz) on multiplié 12 fois par ¹²√2 soit (¹²√2.¹²√2.¹²√2...) = (¹²√2)¹² = 2.
3. Le timbre d’un instrument est en fait sa richesse harmonique : un La de trompette n’est pas un La de piano. Remarque : pour un piano à queue on doit accorder jusqu’à 4 cordes par notes pour faire un accord parfait (Do Mi Sol Do par exemple) que nous entendons comme une seule note mais qui à l’évidence n’est pas une note de guitare (une seule corde).
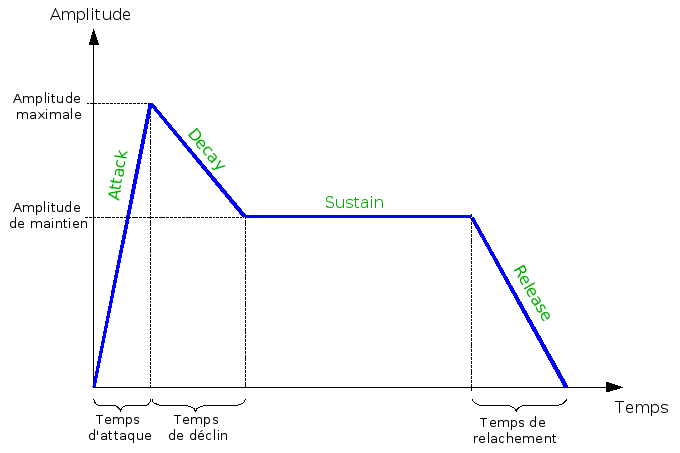
4. L’enveloppe temporelle dépend de la manière dont le son évolue en fonction du temps : une corde peu être pincée (guitare, clavecin), frottée par un archet (violon) ou frappée par un marteau (piano).