1. Logarithme décimal ou népérien ?

• C’est presque pareil : log(x) = ln(x)/ln(10) ce qui permet d’avoir log(10^x) = x au lieu de ln(e^x) = x (e ≈2,71).

• Autres relations amusantes :
  log(1) = ln(1) = 0
  log(ab) = log(a) + log(b) et log(a/b) = log(a) - log(b)

2. Une échelle logarithmique ?

• Le logarithme décimal est utilisé pour des échelles logarithmiques comme en chimie pour les pH, ou en acoustique pour les décibels (car nos oreilles sont logarithmiques), ou pour placer sur un même graphique des longueurs allant de 10^-10 m (atome) à 10¹¹ m (distance Terre-Soleil).
• Comment ? Observer la courbe y = log(x) depuis le point d’abscisse 1 : pour x < 1 elle devient très verticale (variation très rapide) et pour x > 1 elle devient presque horizontale (variation très lente). Le résultat est une dilatation des valeurs très petites et une compression des valeurs très grandes : tout tient sur le même graphique.

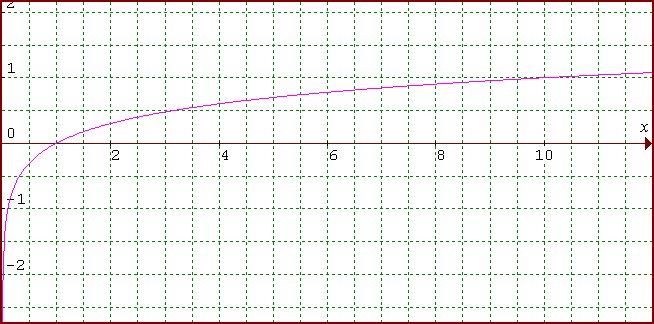
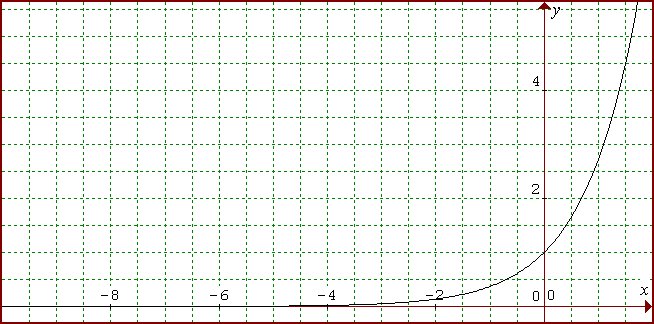
3. L’exponetielle est la fonction inverse du logarithme.