Physique et Chimie au lycée Jan Neruda de Prague
Vive les sciences !
Accueil > Cours de Physique > 1ère année > 1C Cvičení na pohyby - přidána řešení
1C Cvičení na pohyby - přidána řešení
jeudi 22 octobre 2009 par
Několik cvičení na pohyby, výpočty rychlostí, uražených vzdáleností, časů apod.
1. Velká cena Maďarska ve formuli 1 se jezdí na okruhu Hungaroring, který je dlouhý 4381 m a závod se jede na 70 kol.V roce 2008 celý závod vyhrál Heikki Kavalainen v čase 1h 37 min 27,067 s, ale nejrychlejší kolo zajel Kimi Räikkönen za 1 min 21,195 s. Porovnejte jejich průměrné rychlosti a vyslovte závěr.
2. Rychlý posel (běžec) vyrazil s důležitou zprávou. Prvních 5 km svěže utíkal průměrnou rychlostí 15 km/h, což ovšem trochu přepískl, takže další 3 km už jen šel rychlostí 8 km/h a poslední 4 km se již jen vlekl rychlostí 5 km/h. Za jak dlouho urazil celou trasu ? Jaká byla jeho průměrná rychlost na celé trase. Za jak dlouho by dorazil do cíle, pokud by býval celou trasu urazil v počátečním tempu ?
3. Automobil jede po silnici z Prahy do Tábora (80 km). Prvních 40 km to jde dobře a jede průměrnou rychlostí 100 km/h, ovšem druhých 40 km jsou práce na silnici a jeho průměrná rychlost na tomto úseku činí jen 40 km/h. Jaká je jeho průměrná rychlost na celém úseku z Prahy do Tábora ?
4. Nákladní vlak vyrazí z Prahy směrem na Českou Třebovou v 8 hodin 30 minut a jede stálou rychlostí 50 km/h. V 9 hodin 10 minut za ním vyrazí rychlík jedoucí stálou rychlostí 90 km/h. Kdy a kde (jak daleko od Prahy) bude rychlík předjíždět nákladní vlak ? Doplňující zeměpisná otázka : mezi jakými dvěma stanicemi to bude ?
5. V 8.53 vyjíždí z Prahy do Bohumína rychlík jedoucí stálou rychlostí 90 km/h. V 9.26 vyjíždí rychlík z Bohumína do Prahy jedoucí stálou rychlostí 100 km/h. Kdy a kde (v jaké vzdálenosti od Prahy či Bohumína) se budou míjet ? Mezi kterými dvěma stanicemi to bude ? Vzdálenost Praha-Bohumín je 364 km.
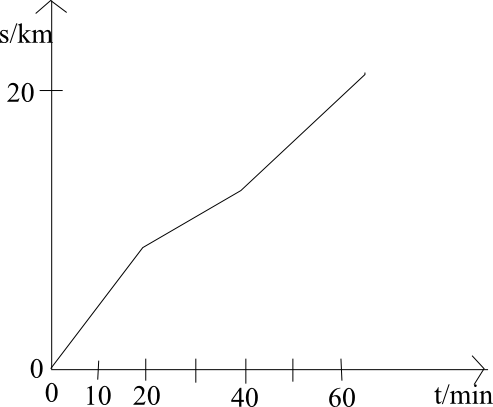
6. V následujícím grafu je zachycena závislost dráhy uražené cyklistou na čase.
a) Ve kterých úsecích je pohyb cyklisty rovnoměrný ?
b) Jakou vzdálenost měl cyklista za sebou v čase 50 minut ?
c) Za jak dlouho ujel prvních 10 km ?
d) Jakou rychlostí se pohyboval v čase 30 minut ? 45 minut ?
e) Jakou průměrnou rychlostí se pohyboval v prvních 40 minutách ?
f) Jakou průměrnou rychlostí se pohyboval na prvních 5 kilometrech ?
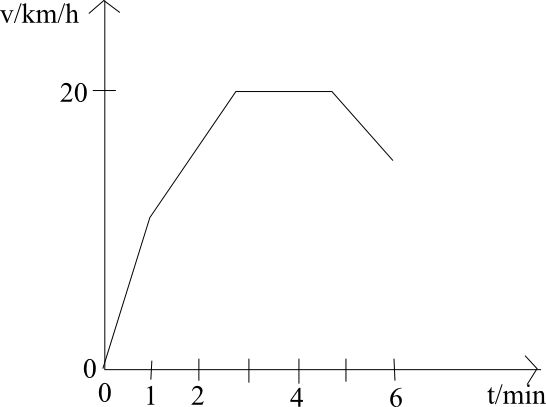
7. V následujícím grafu je zachycena závislost rychlosti cyklisty na čase.
a) Ve kterých úsecích je pohyb cyklisty rovnoměrný ? zrychlený ? zpomalený ?
b) Jakou rychlostí se pohyboval v čase 1 minuta ? 4 minuty ?
c) Za jak dlouho poprvé dosáhl rychlosti 15 km/hod ?
d) Jakou vzdálenost měl cyklista za sebou v čase 1 minuta ? 5 minut ?
e) Za jak dlouho ujel první 1 km ?
f) Jakou průměrnou rychlostí se pohyboval v prvních 4 minutách ?
g) Jakou průměrnou rychlostí se pohyboval na prvním 1 kilometru ?
8. Převody jednotek délky, rychlosti a času :
a) 2,5 hod = min = s
b) 2500 s = hod = min
c) 3,5 ms = s = min
d) 9,5 hod = s = min
e) 28 min = hod = s
f) 2 dny = hod = min = s
g) 3,5 km = m = cm
h) 350 m = mm = m
i) 8000 mm = m = cm
j) 95 cm = m = mm
k) 3,6 km/h = m/s
l) 5,6 m/min = m/s = km/h
m) 3,1 km/s = m/s = km/h
n) 63 m/s = km/h
o) 10 cm/s = m/s = km/h
p) 29 km/den = m/s = km/h
q) 100 m/hod = m/s = km/h
r) 23cm/h = m/s = km/h
s) 36 uzlů = m/s = km/h (1 uzel je 1 námořní míle za hodinu ; 1 námořní míle = 1852 m)
t) 50 km/h = uzlů
u) 100 mph = m/s = km/h ( mph je mile per hour (míle za hodinu ; 1 míle je 1609 m)
v) 6 stop 5 palců = m (1 stopa je 30,5 cm, 1 palec je 2,54 cm)
w) 50 miles = km
x) 5000 km = námořní míle
y) 30 mm/min = cm/h = m/s = km/h
z) 80 cm/den = m/s = km/h
Řešení nebo náznaky řešení úloh :
1. Jednoduché, stačí si vždy spočítat uraženou dráhu a vydělit ji časem jízdy. Je třeba převést jednotky !
Výsledky : Kavalainen 52,4 m/s, Raikkonen 54,0 m/s.
2.Je třeba sečíst doby, ze které urazil jednotlivé úseky (to je vždy podíl dráhy a času) ; průměrná rychlost je podíl celkové dráhy a celkové doby ; teoretický čas v poslední otázce je podílem celkové dráhy a první rychlosti.
Výsledky : 1,5 h ; 8 km/h ; 0,8 h
3. Je třeba napřed spočítat celkovou dobu pohybu a tou pak vydělit celkovou uraženou dráhu.
Výsledek : 57 km/h
4. Je třeba spočítat, kolik ujede nákl. vlak do okamžiku, než vyrazí rychlík (jede 40 min = 2/3 hod rychlostí 50 km/h, ujede tedy 2/3.50 km = 33 km). Pak se na celou situaci budeme dívat z hlediska nákladního vlaku - ten se vůči sobě nepohybuje, zatímco rychlík se vůči němu pohybuje rycjhlostí 90-50=40 km/h. Za jak dlouho urazí 33 km - počáteční vzdálenost mezi vlaky ? Za 33/40 h =0,83 h. Kolik za tu dobu ujede (vůči zemi, tj. rychlostí 90 km/h) ? 0,83.90 km = 75 km. Rychlík dožene nákl. vlak 75 km od Prahy v čase 9h10min+0,83h = 9h10min + 0,83.60min = 10h0min. Dle jízdního řádu to bude v Týnci nad Labem.
5.Opět je třeba spočítat, kolik ujede rychlík z Prahy do okamžiku, než vyrazí rychlík z Bohumína (jede 33 min - 0,55 hod rychlostí 90 km/h, ujede tedy 0,55.90 km = 49,5 km). Pak se na celou situaci budeme dívat z hlediska rychlíku z Bohumína - ten se vůči sobě nepohybuje, zatímco rychlík z Prahy se vůči němu pohybuje rycjhlostí 90+100=190 km/h. Za jak dlouho urazí 364-49,5=314,5 km - počáteční vzdálenost mezi vlaky ? Za 314,5/190 h =1,66 h. Kolik za tu dobu ujede (vůči zemi, tj. rychlostí 100 km/h) ? 1,66.100 km = 166 km. Rychlík z Bohumína potká rychlík z Prahy 166 km od Bohumína, tj. 364-166=198 km km od Prahy v čase 9h26min+1,66h = 9h26min + 1,66.60min = 11h06min. Dle jízdního řádu to bude mezi Hoštejnem a Lupěným.
6. a) Ve všech znázorněných úsečkou, tedy 0-20 min, 20-40 min, 40-70 min
b) Odhaduji tak 16 km
c) Odhaduji tak 30 min
d) To jel zrovna rovnoměrným pohybem mezi 20 - 40 min. Za těchto 20 minut = 1/3 hod urazil tak 4 km (viz graf), rychlost tedy byla 4:1/3 = 12 km/h.
To jel zrovna rovnoměrným pohybem mezi 40 - 70 min. Za těchto 30 minut = 0,5 hod urazil tak 10 km (viz graf), rychlost tedy byla 10:0,5 = 20 km/h.
To jel zrovna rovnoměrným pohybem mezi 40 - 70 min. Za těchto 30 minut = 0,5 hod urazil tak 10 km (viz graf), rychlost tedy byla 10:0,5 = 20 km/h.
e) Za 40 minut = 2/3 hod urazil tak 12 km, rychlost je tedy 12:2/3 = 18 km/h
f) 5 km urazil tak za 15 min(=0,25 hod), rychlost je tedy 5:0,25=20 km/h
Pozn : Výsledky jsou orientační, odhaduji jen na monitoru.
7.a) rovnoměrný - v=konst - 3-5 min
zrychlený - v roste - 0-3 min
zpomalený - v klesá - 5-6 min
b) - podívám se, jaká v odpovídá příslušnému času ; 10 km/h ; 20 km/h
c) Za 2 min
d) Rychlosti převést na km/min. Dráha je plocha pod křivkou ; trojúhelník - 1.0,17/2=0,085 km ; trojúhelník + lichoběžník (tj. obdélník + trojúhelník) + obdélník - 1.0,17/2+(2.0,17+2.0,17/2)+0,34.2=1,28 km
e) Jelikož za 5 minut ujel 1,28 km a poslední 2 minuty z toho jel rovnoměrně rychlostí 0,34 km/min, stačí od času 5 min odečíst čas, za který ujel posledních 0,28 km rychlostí 0,34 km/min, tj 0,28/0,34=0,8 min. Prní kilometr tedy ujel za 5-0,8=4,2 min.
f) Jelikož za 4,2 min ujel 1 km, rychlost je zhruba 1/4,2 km/min=0,24 km/min = 14 km/h
g) To samé jako otázka e)
Pozn. Otázky e, f, g jsou poměrně obtížné - nebudou jako základní učivo vyžadovány.
Contact |
Se connecter |
Plan du site |
Mentions légales |
 RSS 2.0 |
Haut de page |
RSS 2.0 |
Haut de page |
 |
|
Physique et Chimie au lycée Jan Neruda de Prague (Lycée Bilingue Jan Neruda)